COMSOL has the best multiphysical simulation capabilities in my experience. Technical support from Elisa at TECHNIC as well as the engineers at COMSOL has been great.
COMSOL is an important part of our research in plasma physics. We use it in the design of plasma systems and it helps us to obtain a greater understanding of the underlying physics. We have always valued the quick support from TECHNIC and COMSOL and it has been a pleasure to work with them.
Comsol has become a valuable part of our design and decision making process. The exceptional flexibility and access to the physics and solvers in Comsol has allowed us to have deeper understanding on thermomechanical solutions. Technic and Comsol have always been quick and helpful to resolve any issues and provide helpful advice on their products.
At Scion we use COMSOL Multiphysics to understand energy processes, such as the interplay of non-linear solid mechanics and heat & mass transfer during biomass compaction, to design new or more efficient processes.
We use COMSOL Multiphysics to design the customised muffler. With it, we can simulate the insertion loss at different spectrum with different muffler designs.
The Optimisation Module is an add-on package that you can use in conjunction with any existing COMSOL Multiphysics Product. Once you have created a COMSOL Multiphysics model of your product or process, you always want to improve on your design. This involves four steps. First, you define your objective function – a figure of merit that describes your system. Second, you define a set of design variables – the inputs to the model that you would like to change. Third, you define a set of constraints, bounds on your design variables, or operating conditions that need to be satisfied. Last, you use the Optimisation Module to improve your design by changing the design variables, while satisfying your constraints. The Optimisation Module is a general interface for defining objective functions, specifying design variables, and setting up these constraints. Any model input, whether it be geometric dimensions, part shapes, material properties, or material distribution, can be treated as a design variable, and any model output can be used to define the objective function. It can be used throughout the COMSOL Multiphysics product family and can be combined with the LiveLink™ add-on products to optimise a geometric dimension in a third-party CAD program.
A horn originally had the shape of an axisymmetric cone with a straight boundary. This is optimised with respect to the far-field sound pressure level.
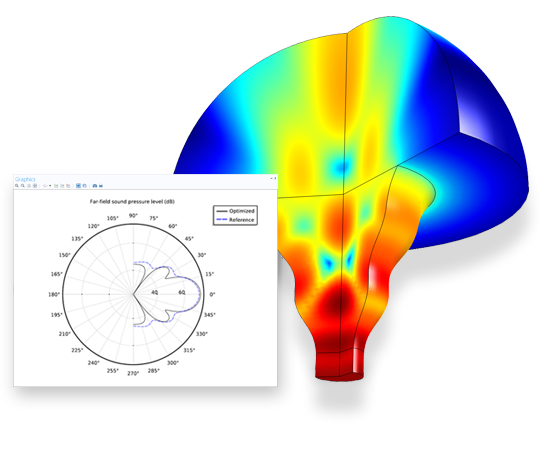
The Optimisation Module includes two different optimisation techniques: Derivative-Free and Gradient-Based optimisation. Derivative-Free optimisation is useful when your objective functions and constraints may be discontinuous and do not have analytic derivatives. For example, you may want to minimise the peak stress in your part by changing the dimensions. However, as the dimensions change, the location of the peak stresses can shift from one point to another. Such an objective function is non-analytic and requires a derivative-free approach. Five such methods are available in the Optimisation Module: the Bound Optimisation by Quadratic Approximation (BOBYQA) method, the Constraint Optimisation by Linear Approximation (COBYLA) method, the Nelder-Mead method, the coordinate search method, and the Monte Carlo method.
The Optimisation Module will compute an approximate gradient to evolve the design variables towards an improved design. You may want to minimise the total mass of your part which can also be done using this approach. The mass of the part is usually directly differentiable with respect to the part dimensions, permitting use of a gradient-based approach. The Optimisation Module will compute the exact analytic derivative of your objective and constraint functions using the adjoint method of the SNOPT optimiser, developed by Philip E. Gill of the University of California San Diego and Walter Murray and Michael A. Saunders of Stanford University, to improve the design variables. A second gradient-based algorithm is a Levenberg-Marquardt solver. You can use this solver when the objective function is of a least-squares type, typically for parameter estimation and curve fitting applications. A third method, the Method of Moving Asymptotes (MMA), is a gradient-based optimisation solver written by Professor K. Svanberg at the Royal Institute of Technology in Stockholm, Sweden. It is designed with topology optimisation in mind. The method is called GCMMA in the literature and is available in the Optimisation Module under the name MMA.
The advantage of the gradient-based method is that it can address problems involving hundreds, or even thousands, of design variables with very low increase in computational cost as the number of design variables increases. The Adjoint method simultaneously computes all analytic derivatives, whereas the derivative-free method has to approximate each derivative, and will take more time as the number of design variables increases. The gradient-based methods can also include more complex constraint functions.
The advantage of the derivative-free method is in its simplicity. It does not require finding a differentiable objective function, and it requires less user interaction to set up. However, due to the computational costs, derivative-free methods are most attractive when the number of design variables is around 10 or less. In practice, this covers a wide range of practical engineering optimisation problems.
Parameter Optimisation involves optimising any scalar input to the model, such as flow rates and load magnitudes. This is usually the easiest kind of optimisation and can be addressed with any technique.
Parameter Estimation is more complex, and involves correlating a COMSOL model to experimental data. Typically, the objective is to use a model to estimate material properties used.
Optimisation methods can be further classified by the types of variables being optimised. Dimension, Shape, and Topology optimisation are all addressed within the Optimisation Module, and each has its own place in the design process.
Dimensional optimisation involves defining design variables that can be directly translated to manufacturing. Typical design variables may be hole sizes, or length, width, and height of structural members. Dimensional optimisation is usually used as the last step in the design process and is performed once the design is more or less fixed in terms of the overall shape. The derivative-free method is usually used here.
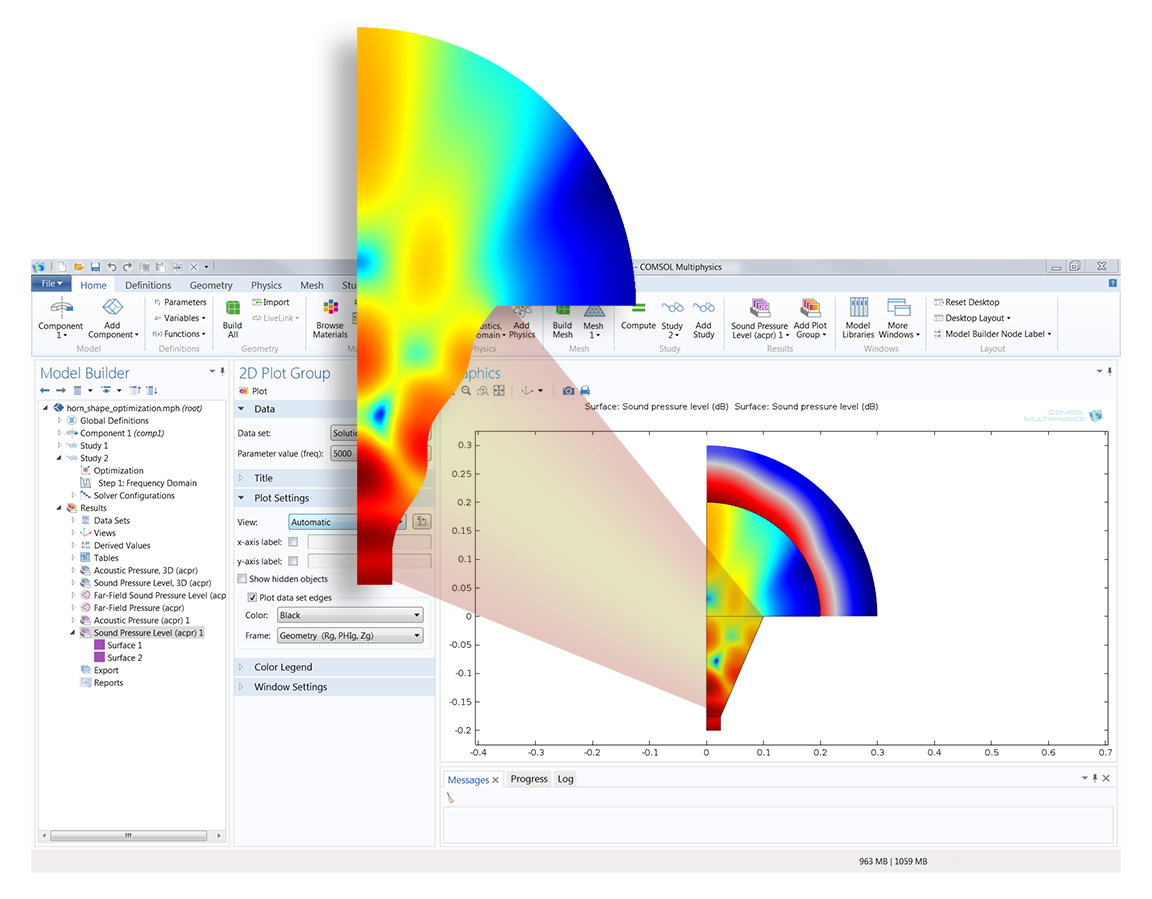
Shape optimisation typically occurs earlier in the design process, and involves a more free-form alteration of the object. More care is usually required for choosing the design variables, as the objective is to improve the shape without over-constraining the design. The gradient-based method is preferred if an analytic objective function can be found.
Topology optimisation is used very early in the design process, typically in the conceptual stage. Topology optimisation treats the distribution of material as a design variable and inserts or removes structures to improve the objective function. Due to the high number of design variables, only gradient-based optimisation is practical.
In order to fully evaluate whether or not the COMSOL Multiphysics® software will meet your requirements, you need to contact us. By talking to one of our sales representatives, you will get personalised recommendations and fully documented examples to help you get the most out of your evaluation and guide you to choose the best license option to suit your needs.
Fill in your contact details and any specific comments or questions, and submit. You will receive a response from a sales representative within one business day.