COMSOL has the best multiphysical simulation capabilities in my experience. Technical support from Elisa at TECHNIC as well as the engineers at COMSOL has been great.
COMSOL is an important part of our research in plasma physics. We use it in the design of plasma systems and it helps us to obtain a greater understanding of the underlying physics. We have always valued the quick support from TECHNIC and COMSOL and it has been a pleasure to work with them.
Comsol has become a valuable part of our design and decision making process. The exceptional flexibility and access to the physics and solvers in Comsol has allowed us to have deeper understanding on thermomechanical solutions. Technic and Comsol have always been quick and helpful to resolve any issues and provide helpful advice on their products.
At Scion we use COMSOL Multiphysics to understand energy processes, such as the interplay of non-linear solid mechanics and heat & mass transfer during biomass compaction, to design new or more efficient processes.
We use COMSOL Multiphysics to design the customised muffler. With it, we can simulate the insertion loss at different spectrum with different muffler designs.
The study of rotordynamics is important in application areas that involve rotating machinery, such as the automotive and aerospace industries, power generation, and the design of electrical products and household appliances. The physical behaviour of rotating machines is greatly influenced by vibrations, which are exacerbated by the rotation and structure of the machines themselves. Perfectly symmetrical rotor assemblies exhibit different natural frequencies as a function of rotational speed, while imperfections and unbalances can excite these frequencies in intricate ways. When designing machinery with rotating parts, you need an efficient way to consider these behaviours and optimise operation and performance.
You can use the Rotordynamics Module, which is an expansion to the Structural Mechanics Module, to analyse the effects of lateral and torsional vibrations of rotating machinery in order to study rotor vibrations and contain their levels within acceptable design limits. Among the different design parameters you can evaluate with this module are critical speeds, whirl, natural frequencies, stability thresholds, and the stationary and transient responses of a rotor due to mass unbalances. You can also see how rotational behaviour may lead to stresses in the rotor itself, as well as additional loads on and vibration transmissions to other parts of the rotating machine's assembly.
With the Rotordynamics Module, you can take into account the effects of various stationary and moving rotor components, including disks, bearings, and foundations. You can also easily postprocess your results directly within the software environment, presenting them as Campbell diagrams, modal orbits, harmonic orbits, waterfall plots, and whirl plots.
With the COMSOL Multiphysics® simulation platform and its add-on modules, you have access to a set of predefined modelling tools called physics interfaces, which are tailored to specific areas of analyses. The Rotordynamics Module provides five dedicated physics interfaces that you can use to accurately model rotors and bearings:
By using the multiphysics couplings available in the Rotordynamics Module, you are able to capture the effect of oil whirl and whip through coupling the physics in the Hydrodynamic Bearing interface to those in the Beam Rotor and Solid Rotor interfaces.
Additionally, you can combine the Rotordynamics Module with other modules in the COMSOL product suite for coupled and multiphysics simulations. This means that you can examine how other types of physics affect your rotordynamics designs. For example, by combining the Rotordynamics Module with the Multibody Dynamics Module, you can perform a transient simulation to predict the vibrations in a geared rotor assembly for an externally applied torque.
The pressure distribution in the lubricant of the bearings (rainbow colour plot), von Mises stresses (blue colour plot), and displacement of the bearings (Orbit plot) resulting from a rotordynamics analysis.
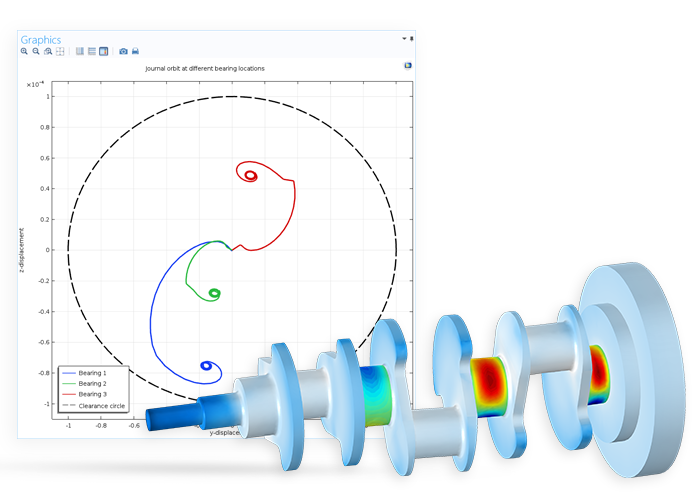
To achieve the most accurate description of a rotating machinery assembly, you need to be able to consider all of its participating components. You can use the most general approach to modelling such assemblies, traditional finite element analysis, with the Solid Rotor interface in the Rotordynamics Module. With this approach, you represent the rotor with a 3D geometry and use solid elements to define the rotor assembly.
In the Solid Rotor interface, you can include full descriptions of geometrical asymmetries and unbalances in your analysis, as well as nonlinear geometric effects. You can also account for deformations in journals and mountings, consider gyroscopic effects, and capture the effects of spin softening and stress stiffening in your simulation. This interface is most useful if you need explicit simulation results for deformation and stresses in the rotor and its components.
Bearings and foundations are essential to a rotor assembly; they are the components that connect a rotor to its surrounding parts. Rotor system responses are very sensitive to the type of bearing or foundation, so you need to be able to accurately describe their behaviour. Dedicated interfaces and features within the Rotordynamics Module make these components easy to define.
Journal bearings restrict the translational motion of a journal in the lateral direction and its rotation about both lateral axes due to the finite length of the journal. There are two options for modelling journal bearings: either as a full hydrodynamic bearing, with a detailed description of the lubricant's pressure and flow, or by making approximations using lumped models.
With lumped models, you can simulate the following varieties of journal bearings and their behaviour in the Rotordynamics Module:
You can model the behaviour of journal bearings in detail with the Hydrodynamic Bearings interface. The interface includes predefined physics that make it easy to model the oil between a journal and bushing that acts as a lubricant by solving the Reynolds equation.
You can use this interface to analyse a journal bearing and its characteristics in terms of stiffness and damping, or in a multiphysics coupling with the Solid Rotor or Beam Rotor interface to study the dynamics of the full rotor assembly. These interfaces provide built-in models for the following hydrodynamic bearing types:
To analyse thrust bearings, which restrict the axial motion of a rotor and the rotation about the lateral axes, you can use lumped parameters. You are able to model the following varieties of thrust bearings and their behaviour in the Rotordynamics Module:
Bearing foundations are the structural components on which bearings rest. You can model foundations in your rotor assembly design as:
With the range of study types included in the Rotordynamics Module, you can properly analyse the dynamics of a rotor assembly using different analysis techniques that are adapted to the characteristics of rotordynamics phenomena.
The Rotordynamics Module enables you to account for gyroscopic effects, including frame acceleration forces. In the module, the vibrational effects are modelled from the perspective of a corotating observer by using a coordinate system that is rotating in sync with the rotor. This simplifies your modelling process, as you do not need to know the actual physical rotation of the rotor in order to simulate the assembly.
From the perspective of a corotating frame, conventional intuition of what is a stationary versus dynamic force no longer applies. In a rotordynamics analysis, inertial effects may appear as stationary forces, whereas a gravity force, which is stationary in a traditional analysis, appears as a dynamic sinusoidally varying force seen from a corotating frame. In this way, a stationary study has a different interpretation in rotordynamics than in conventional analyses.
The vibrational modes of a rotor will travel in an orbit in either the direction of the rotor's rotation (forward whirl) or the opposite direction (backward whirl). This phenomenon can be analysed using various eigenfrequency and frequency domain studies, as well as by performing a fully transient analysis using a time domain study.
In the Rotordynamics Module, you can use the following study types for both static and dynamic analyses:
In order to fully evaluate whether or not the COMSOL Multiphysics® software will meet your requirements, you need to contact us. By talking to one of our sales representatives, you will get personalised recommendations and fully documented examples to help you get the most out of your evaluation and guide you to choose the best license option to suit your needs.
Fill in your contact details and any specific comments or questions, and submit. You will receive a response from a sales representative within one business day.
Tel: +61 (03) 6224 8690Email: info@technic.auConnect on LinkedInGet Your Free TrialCopyright © 2021 Technic Pty Ltd. All Rights Reserved. See our Privacy Policy. Site protected by reCAPTCHA - Privacy | Terms. Website by Gloo.
